Manejo de numeros complejos en python

Recordemos que cuando queremos resolver ciertas ecuaciónes tales como \(x^2 + 1=0\) estas no tienen solución.

Para esto en matematicas se introducen los números complejos que son numeros de la forma \(z=x+ i y\)

Python trae por defecto una forma de utilizar estos numeros complejos. Veamos esto en codigo para entender su introducción.

###### Para python la unidad imaginaria "i" se escribe como "1j"
unidad_imaginaria = 1j
# Luego, podemos inicializar un numero complejo de 2 maneras

# Manera EXPLICITA : z=a+bj 
c_1 = 3+5j
# Manera IMPLICITA : z=(x,y)
c_2 = complex(3,5)
print("Variable   \t " , " " ,"|" , " " ,"Tipo de Dato")
print("--------------------|----------------------")
print(f"{c_1}      \t " , " " ,"|" , " " ,  type(c_1))
print(f"{c_2}      \t " , " " ,"|" , " " ,  type(c_2))

Variable   	    |   Tipo de Dato
--------------------|----------------------
(3+5j)      	    |   <class 'complex'>
(3+5j)      	    |   <class 'complex'>

# Con respecto a las operaciones. Python se encarga de identificar si es o no complejo
c_3 = unidad_imaginaria + c_1
c_4 = unidad_imaginaria - c_1
c_5 = unidad_imaginaria * c_1
c_6 = unidad_imaginaria / c_1

print("Variable   \t " , " " ,"|" , " " ,"Operacion \t" , " " ,"|" , " ", "Resultado")
print("--------------------|----------------------|-----------------")
print("c_3      \t " , " " ,"|" , " " ,f"{unidad_imaginaria}+ {c_1} \t", " " ,"|" , " " , c_3)
print("c_4      \t " , " " ,"|" , " " ,f"{unidad_imaginaria} - {c_1} \t", " " ,"|" , " " , c_4)
print("c_5      \t " , " " ,"|" , " " ,f"{unidad_imaginaria} * {c_1} \t", " " ,"|" , " " , c_5)
print("c_6      \t " , " " ,"|" , " " ,f"{unidad_imaginaria} / {c_1} \t", " " ,"|" , " " , c_6)

Variable   	    |   Operacion 	   |   Resultado
--------------------|----------------------|-----------------
c_3      	    |   1j+ (3+5j) 	   |   (3+6j)
c_4      	    |   1j - (3+5j) 	   |   (-3-4j)
c_5      	    |   1j * (3+5j) 	   |   (-5+3j)
c_6      	    |   1j / (3+5j) 	   |   (0.14705882352941177+0.08823529411764706j)

# Para tomar la parte real, existe el atributo real
print(c_1.real)
# Para tomar la parte imaginaria, existe el atributo imag
print(c_1.imag)
# Podemos tomar el conjudago de un numero con el metodo conjugate()
print(c_1.conjugate())

3.0
5.0
(3-5j)

Se puede realizar un cambio de coordenadas.

Recordemos que se puede identificar un numero complejo como un punto del plano complejo, donde se toma el eje imaginario como el eje de ordenadas, y al eje real como el de absisas. Ademas, podemos expresar al numero complejo en sus coordenadas polares, la cual es mas util para poder representar los numeros complejos en un eje de coordenadas.

Para hacer un paso de coordenadas de rectangulares a polares utilizaremos la libreria cmath

import cmath as cm

z1 = 3+5j # Esta en cartesianas

# Utilizo la funcion *polar* de cmath para convertir a polares
z1_polar = cm.polar(z1) 

# Ahora, para tomar la tupla de coordenadas polares y convertirlo a numero complejo 
# utilizamos la función *rect* de cmath
z1_comp = cm.rect(z1_polar[0], z1_polar[1])


print(type(z1_polar)) # Nos debe devolver que es una tupla
print(z1_polar)       # (modulo, angulo en radianes)
print(type(z1_comp))  # vuelve a ser complejo
print(z1_comp)        # Vuelvo a cartesianas

<class 'tuple'>
(5.830951894845301, 1.0303768265243125)
<class 'complex'>
(3+5j)

Imaginemos que estamos trabajando con numpy y no queremos cargar mas librerias.

Podemos hacer este cambio de coordenadas de la siguiente forma

import numpy as np

z1_modulo, z1_angulo = (abs(z1), np.angle(z1))

print("Coordenadas polares del complejo \n\n")
print(f"Modulo de z1: {z1_modulo} \nAngulo del complejo: {z1_angulo}")

print("\n¿Son iguales los valores obtenidos para ambas representaciónes?")
print(f"--> Modulo de z1: {z1_polar[0] == z1_modulo} \n--> Angulo del complejo: {z1_polar[1]==z1_angulo}")

Coordenadas polares del complejo 


Modulo de z1: 5.830951894845301 
Angulo del complejo: 1.0303768265243125

¿Son iguales los valores obtenidos para ambas representaciónes?
--> Modulo de z1: True 
--> Angulo del complejo: True

Una versatilidad que tiene trabajar con numpy es el hecho de que podemos pedirle que los pase el angulo a grados. Por defecto, este lo pasa en radianes, sin embargo podemos pasarle el atributo deg=True al metodo angle de numpy.

z1_rad = z1_angulo
z1_deg = np.angle(z1, deg=True)

print(f"En radianes: {z1_rad} \n\nEn grados: {z1_deg}")

En radianes: 1.0303768265243125 

En grados: 59.03624346792648

Ahora, recordando que \(z_1 = a+i b = |z_1|e^{i \theta}\) Podemos utilizar el numero de Euler definido en numpy para poder hacer el pase de coordenadas polares a la forma binomica

z1_binomica = z1_modulo * (np.e ** (1j * z1_rad)) # Debe estar en radianes

print(f"La forma binomica es: {z1_binomica}")

La forma binomica es: (3+5j)

import matplotlib.pyplot as plt

def move_spines():
    """Crea la figura de pyplot y los ejes.
       Mueve las lineas de la izquierda y de abajo
       para que se itersecten con el origen. 
       Elimina las lineas de la derecha y de arriba
       Devuelve los ejes"""
    
    fix, ax = plt.subplots()
    
    for spine in ["left", "bottom"]:
        ax.spines[spine].set_position("zero")
    
    for spine in ["right", "top"]:
        ax.spines[spine].set_color("none")
    
    return ax

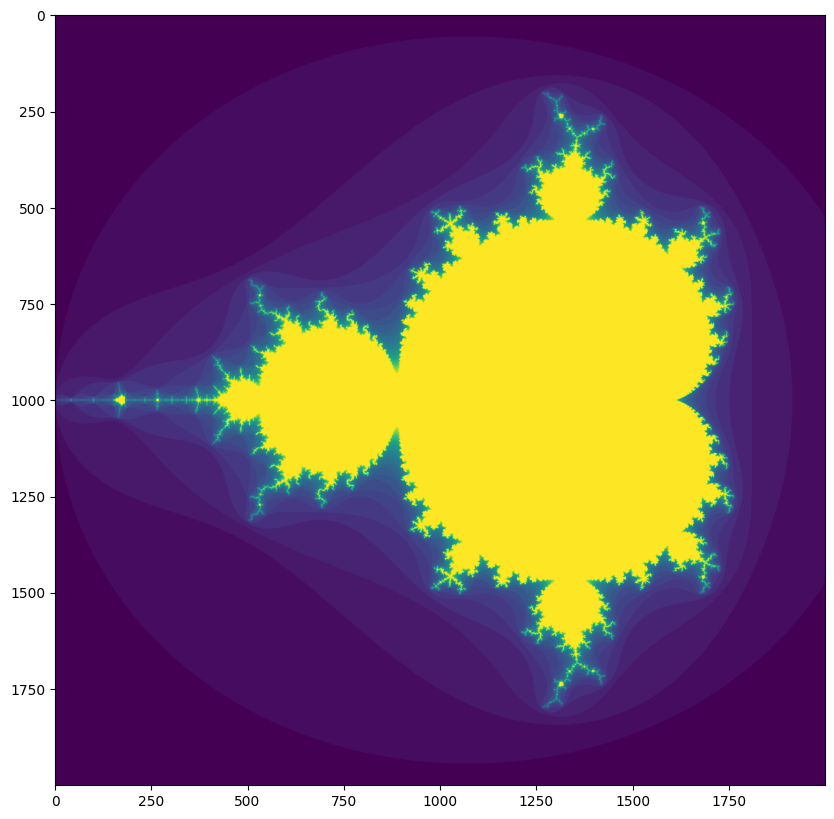
# Defino un numero Complejo
z = 3 + 4j

# LLamamos a la funcion
ax = move_spines()
ax.set_xlim(-5,5)
ax.set_ylim(-5,5)
ax.grid()
ax.scatter(z.real,z.imag)
plt.title("Grafico del punto en el plano complejo")
plt.show()

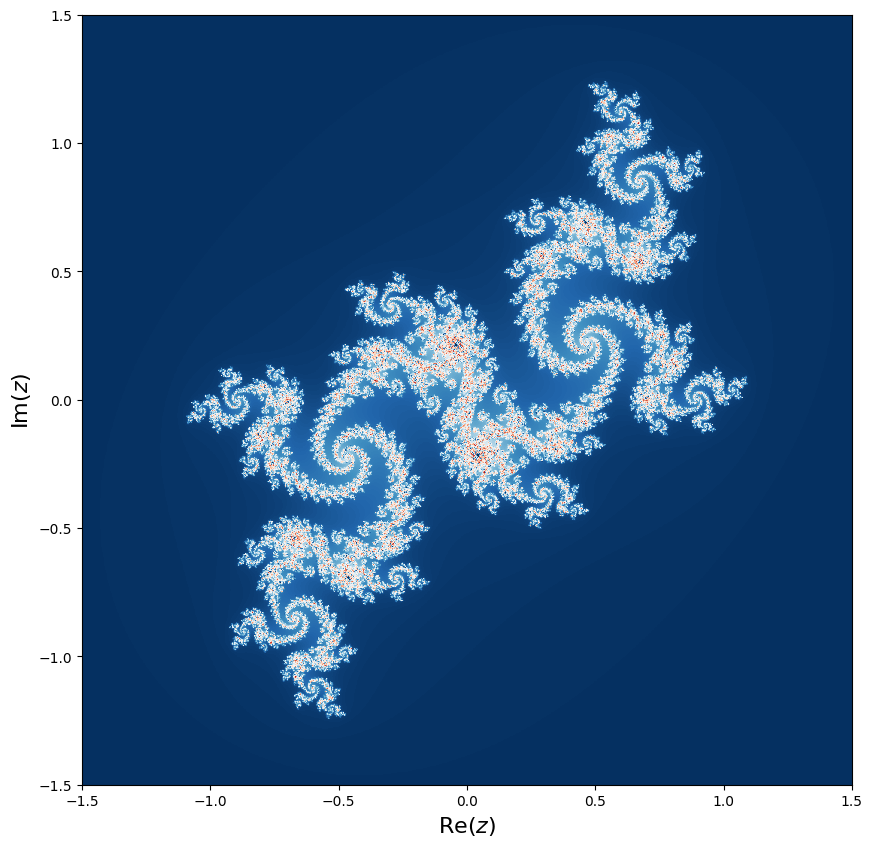
Los numeros complejos nos permiten graficar fractales. Veamos un ejemplo para graficar conjuntos de Julia.

Para esto implementaremos un programa con numpy y numba

import numba

def py_julia_fractal(z_re, z_im, j):
    """Crea el grafico del fractal de Julia."""
    
    for m in range(len(z_re)):
        for n in range(len(z_im)):
            z = z_re[m] + 1j * z_im[n]
            
            for t in range(256):
                z = z ** 2 - 0.05 + 0.68j
                if np.abs(z) > 2.0:
                    j[m,n] = t
                    break

jit_julia_fractal = numba.jit(nopython=True)(py_julia_fractal)

N = 1024
J = np.zeros((N, N), np.int64)
z_real = np.linspace(-1.5, 1.5, N)
z_imag = np.linspace(-1.5, 1.5, N)

jit_julia_fractal(z_real, z_imag, J)

fig, ax = plt.subplots(figsize=(10,10))

ax.imshow(J, cmap=plt.cm.RdBu_r, extent=[-1.5, 1.5, -1.5, 1.5])
ax.set_xlabel("$\mathrm{Re}(z)$", fontsize=16)
ax.set_ylabel("$\mathrm{Im}(z)$", fontsize=16)

Text(0, 0.5, ‘$\mathrm{Im}(z)$’)

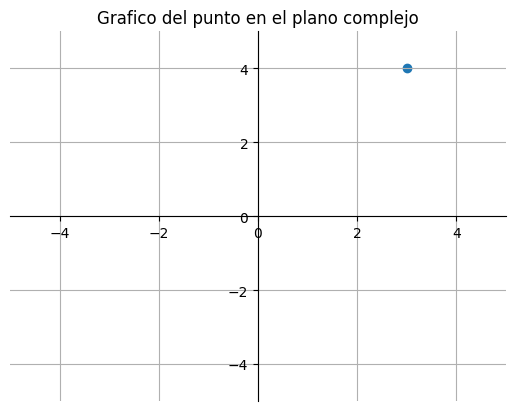
Otro ejemplo de fractal es el conjunto de Malderbrot

def mandelbrot(h, w, maxit=20):
    """Crea el grafico Fractal de Mandelbrot del tamaño (h,w)"""
    
    y, x = np.ogrid[-1.4:1.4:h*1j, -2:0.8:w*1j]
    
    c = x + y*1j
    z = c
    
    divtime = maxit + np.zeros(z.shape, dtype=int)
    
    for i in range(maxit):
        z = z**2 + c
        
        diverge = z*np.conj(z) > 2**2
        div_now = diverge & (divtime==maxit)
        
        divtime[div_now] = i
        
        z[diverge] = 2
    
    return divtime
    
plt.figure(figsize=(10,10))
plt.imshow(mandelbrot(2000,2000,30))
plt.show()