Osilaciones Forzadas

Vamos a ver cómo resolver el ejercicio 9 de la guía de repaso, esto nos va a ayudar a repasar el oscilador amortiguado y el forzado. Además vamos a usar algunas funciones de python para acostumbrarnos a esta nueva (para algunxs) herramienta.

Tenemos un problema unidimensional de una masita $m$ engarzada a un resorte de constante elástica $k$ y longitud natural \(l_0\). Podemos suponer que está inmerso en un fluido viscoso con constante \(\gamma\). El enunciado de la guía nos sugiere que utilicemos \(k=m\omega_0 ^2\) y \(\Gamma=\gamma/m\).

En física 1 solían poner el eje x con el origen en la pared.

Lo primero que tenemos que hacer entonces es escribir la ecuación de Newton: \begin{equation} m\ddot{x}=F_{elas}+F_{visc} \end{equation}

Las únicas fuerzas presentes son la elástica y la viscosa, las escribimos explícitamente, recuerden que ambas son restitutivas.

\begin{eqnarray} m\ddot{x}=-k(x-l_0)-\gamma \dot{x}
\implies \ddot{x}=-\omega_0^2x-\Gamma \dot{x}+l_0\omega_0^2 \end{eqnarray}

En el último paso reescribimos la ecuación de Newton con las constantes propuestas por la guía.

Para hacerlo más sencillo, les propongo que este ejercicio lo encaremos con el eje en la posición en la que el resorte está relajado (posición de equilibrio). Además es lo que vamos a hacer durante toda la materia.

Considerando también la fuerza \(F(t)\), pueden ver que la ecuación que queda es

\[\ddot{x} + \Gamma \dot{x} + \omega_0^{2}x = \frac{F_0}{m} \, \cos{\Omega t}\]

Se acuerdan cómo resolver estas ecuaciones? Al ser lineal, la solución más general es la suma de la solución de la ecuación homogénea y una solución particular de esta ecuación tal como la tenemos acá.

Primero resolvamos el sistema homogeneo, cuál es?

\begin{equation} \ddot{x}_h+\omega_0^2x_h+\Gamma \dot{x}_h=0 \hspace{3cm} (1) \end{equation}

Esta ecuación aparece por primera vez en la guía en el ejercicio 5 y ahí el problema nos propone una solución.

La solución que nos dan es \(x_h(t)=Ce^{-t/2\tau}\cos(\omega_1 t+\theta)\). Las constantes \(\omega_1\) y \(\tau\) no las conocemos. Para hallarlas, tenemos que encontrar las derivadas (primera y segunda) de \(x_h\) y reemplazar en (1). Las constantes \(C\) y \(\theta\) van a quedar definidas una vez que explicitemos las condiciones iniciales. Les voy a dejar hechas las derivadas, los pasos intermedios se los dejo a ustedes (es importante que los hagan). \(\left\{\begin{array} \dot{x}_h= -Ce^{-t/2\tau}\left(\frac{1}{2\tau}\cos(\omega_1 t+\theta)+\omega_1\sin(\omega_1 t+\theta) \right ) \hspace{2cm} (2)\\ \ddot{x}_h=Ce^{-t/2\tau}\left[\frac{1}{2\tau}\left (\frac{\cos(\omega_1 t+\theta)}{2\tau}+\omega_1\sin(\omega_1 t+\theta) \right )+\frac{\omega_1}{2\tau}\sin(\omega_1 t+\theta)-\omega_1^2\cos(\omega_1 t+\theta)\right ] \hspace{2cm} (3) \end{array}\right.\)

Ahora tenemos que reemplazar todo en (1). De nuevo, varios pasos intermedios les quedan a ustedes.

\[\begin{eqnarray} 0=\color{#21ABCD}C \color{#FF007F}{e^{-t/2\tau}} \left[\frac{1}{2\tau}\left (\frac{\cos(\omega_1 t+\theta)}{2\tau}+\omega_1\sin(\omega_1 t+\theta) \right )+\frac{\omega_1}{2\tau}\sin(\omega_1 t+\theta) -\omega_1^2\cos(\omega_1 t+\theta)\right ]-\Gamma \color{#21ABCD}C \color{#FF007F}{e^{-t/2\tau}} \left(\frac{1}{2\tau}\cos(\omega_1 t+\theta)+\omega_1\sin(\omega_1 t+\theta) \right ) +\omega_0^2\color{#21ABCD}C \color{#FF007F}{e^{-t/2\tau}} \cos(\omega_1 t+\theta)\end{eqnarray}\]

Los términos que están en color los podemos cancelar dado que toda la ecuación está igualada a \(0\). ¿Deberíamos tener algún cuidado al hacer esto?

Nos queda entonces la siguiente ecuación \begin{equation} \cos(\omega_1 t+\theta)\left (\frac{1}{(2\tau)^2}-\omega_1^2-\frac{\Gamma}{2\tau}+\omega_0^2\right )+\sin(\omega_1 t+\theta)\left (\frac{\omega_1}{2\tau}+\frac{\omega_1}{2\tau}-\Gamma \omega_1 \right )=0 \end{equation}

¿Qué podemos hacer para hallar \(\tau\) y \(\omega_1\)? Escribí de esta forma la ecuación porque sé que \(k_1 \cos(\omega t) + k_2 \sin(\omega t) = 0\) solo es válido para todo \(t\) si \(k_1 = k_2 = 0\). Otra forma de decir esto es que las funciones \(\sin\) y \(\cos\) forman base completa del espacio de funciones (ya vamos a volver con esto). Esto significa que puedo describir la función que quiera como combinación de senos y cosenos. Además, como forman una base completa y lo que tenemos está igualado a cero, la única opción que nos queda es que lo que acompaña a cada una de las funciones sea cero. Podemos hacer una analogía con las bases de vectores. En ese caso, ya sabemos que podemos escribir cualquier vector como combinación lineal de vectores que llamamos linealmente independientes. En este caso pasa lo mismo. Estamos escribiendo el resultado en base de los “autovectores” seno y coseno.

Entonces ahora nos queda un sistema de dos ecuaciones con dos incógnitas bastante sencillo para resolver \(\begin{matrix}\left. \begin{eqnarray} \frac{1}{(2\tau)^2}-\omega_1^2-\frac{\Gamma}{2\tau}+\omega_0^2=0 \\ \frac{\omega_1}{2\tau}+\frac{\omega_1}{2\tau}-\Gamma \omega_1=0 \end{eqnarray} \right\} \implies \color{#FF2052}{\tau=\frac{1}{\Gamma}}, \color{#FF2052}{\omega_1^2=\omega_0^2-\frac{\Gamma^2}{4}} \end{matrix}\) Ahora viene la parte más interesante. Podemos ver que \(\omega_1\) depende de dos parámetros del problema. El tipo de solución del problema va a depender de la relación entre esos parámetros. Tenemos tres casos posibles, \(\omega_1^2>0\), \(\omega_1^2< 0\) y \(\omega_1^2=0\) . Estudiemos los tres casos y grafiquemos las tres soluciones posibles.

Recordamos la forma funcional de la posición de la masita como función del tiempo \(x_h(t)=Ce^{-\Gamma t/2}\cos(\omega_1 t+\theta)\)

1) Caso subamortiguado: \(\omega_0^2>\frac{\Gamma^2}{4}\)

En este caso tenemos el producto de una exponencial que decae y una oscilación. Esperamos que hayan osilaciones en el sistema, pero cada vez más atenuadas por la exponencial hasta que decaiga completamente. Vamos a graficarlo.

import numpy as np #importamos los paquetes necesarios para hacer los gráficos y escribir las funciones.
import matplotlib.pyplot as plt
from matplotlib import pylab, mlab, pyplot
from matplotlib import cm
from matplotlib.colors import ListedColormap, LinearSegmentedColormap

t= np.linspace(0,20,100); #les damos valores a los parámetros
Gamma=0.5; #viscosidad del fluido donde está inmerso el sistema.
w0=2; #w0 depende de la masita y de la constante del resorte.
omega1=np.sqrt(w0**2-Gamma**2/4);
C=1; #theta y C dependen de las condiciones iniciales. Supongamos que son tales que C=1 y theta=0. 
theta=0;

sub_t=np.exp(-Gamma*t/2)*np.cos(omega1*t);
exp_t=np.exp(-Gamma*t/2);
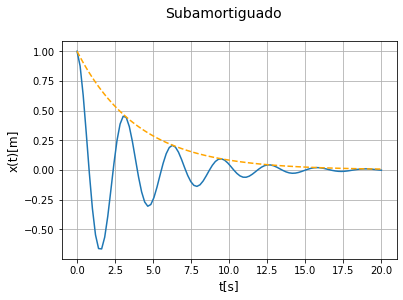
plt.suptitle('Subamortiguado', fontsize=14, y=1)
plt.xlabel('t[s]', fontsize=12)
plt.ylabel('x(t)[m]', fontsize=12)
plt.plot(t, sub_t)
plt.plot(t, exp_t,'--',color = 'orange') #graficamos en línea punteada la exponencial sola.
plt.grid()
plt.show()

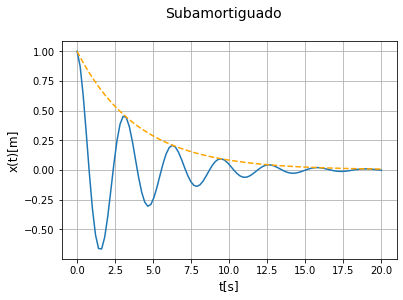
Como vemos, tenemos una oscilación que con el tiempo decae a causa de la exponencial.

Supongamos que estamos haciendo un experimento y podemos cambiar el fluido donde está inmerso el resorte con la masita, es decir, podemos cambiar el \(\Gamma\). Vamos a ver cómo cambia \(x(t)\) a medida que nos aceramos al caso crítico.

t1=np.linspace(0,10,100)
Gamma1=1;
Gamma2=2;
Gamma3=3;
Gamma4=4;
omega_1=omega1=np.sqrt(w0**2-Gamma1**2/4);
omega_2=omega1=np.sqrt(w0**2-Gamma2**2/4);
omega_3=omega1=np.sqrt(w0**2-Gamma3**2/4);
omega_4=omega1=np.sqrt(w0**2-Gamma4**2/4);
sub_t1=np.exp(-Gamma1*t1/2)*np.cos(omega_1*t1);
sub_t2=np.exp(-Gamma2*t1/2)*np.cos(omega_2*t1);
sub_t3=np.exp(-Gamma3*t1/2)*np.cos(omega_3*t1);
sub_t4=np.exp(-Gamma4*t1/2)*np.cos(omega_4*t1);
fig, ax = plt.subplots()
ax.plot(t, sub_t1, label='$\Gamma$=1')
ax.plot(t, sub_t2, label='$\Gamma$=2')
ax.plot(t, sub_t3, label='$\Gamma$=3')
ax.plot(t, sub_t4, label='$\Gamma$=4')
ax.grid()

#ax.axis('equal')
leg = ax.legend();

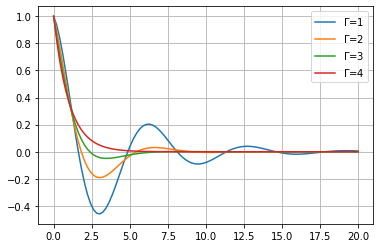
Vemos que a medida que \(\Gamma\) está más cerca del valor que tomamos de \(\omega_0\), el gráfico más se aproxima al de una exponencial decreciente, como lo es en el caso crítico.

2) Caso crítico: \(\omega_0^2=\frac{\Gamma^2}{4}\)

Supongamos que a partir del caso anterior, cambiamos el fluido y llegamos al caso crítico. Es sencillo ver que sólo tenemos la exponencial, dado que el \(\cos(0)=1\).

Se animan a graficarlo ustedes? Les dejamos el esqueleto del código para que piensen el resto ustedes. Fijense en los gráficos anteriores y hagan lo mismo

#Hace falta importar las librerías de nuevo?
#Hace falta definir de nuevo t?
A = 10
B = 10
Gamma_c=2*w0
crit_t= np.exp(-Gamma*t/2)*(A+ B*t) #La exponencial
#Ponele un título al gráfico
plt.xlabel('t[s]', fontsize=12)
plt.ylabel('x(t)[m]', fontsize=12)
plt.plot(t,crit_t)

plt.show()

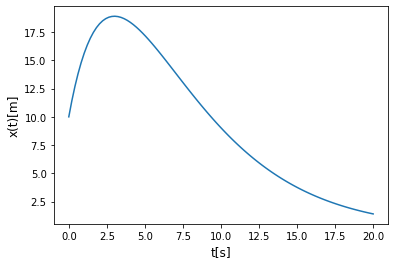
3) Caso sobreamortiguado: \(\omega_0^2<\frac{\Gamma^2}{4}\)

Ahora nuestro problema cambia de régimen. Tenemos un problema (que no es tan problemático en realidad).

Ahora $\omega_1$ es un número complejo!! Escribimos $\omega_1=i|\omega_1|$. Les dejo a ustedes probar que $\cos(ix)=\cosh(x)$. (Probar esto es ejercicio de ustedes).

Para esto recuerden que el coseno hiperbólico se puede escribir como suma de exponenciales (y el coseno?). Para convencerse pueden fijarse en el plot qué pasa si en vez de escribir $np.\cos$, escriben $np.\cosh$

Gamma5=5
omega1_sob=np.sqrt(Gamma5**2/4-w0**2)
sobre_t=np.exp(-Gamma5*t/2)*np.cos(1j*omega1_sob*t);
plt.suptitle('Sobreamortiguado', fontsize=14, y=1)
plt.xlabel('t[s]', fontsize=12)
plt.ylabel('x(t)[m]', fontsize=12)
plt.plot(t, sobre_t.real, 'b')
plt.grid()
plt.show()

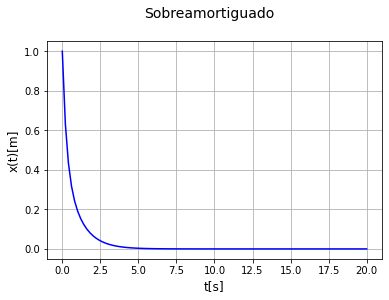
Fijense que a \(t \rightarrow \infty\), todas las soluciones van a cero, es decir que no importa en qué caso estemos, la parte homogenea de la solución va a desaparecer con el tiempo, esto le da el nombre a esta parte de la solución de transitorio. Concentremonos ahora en el término que perdura en el tiempo que lo llamaremos estacionario y lo obtendremos en la solución particular. Hallémosla

\[\ddot{x}_p + \Gamma \dot{x}_p + \omega_0^{2}x_p = \frac{F_0}{m} \cos{\Omega t}\]

¿Cómo resolvemos esto? Haciendole caso a la guía, en este caso al ejercicio 9. El eunciado nos dice que nos da la solución para tiempos suficientemente grandes donde solo existe la parte estacionaria, exactamente lo que estamos buscando.

\[x_p(t) = A \sin{\Omega t} + B \cos{\Omega t}\]

Al igual que lo que hicieron antes, deriven y reemplacen en la ecuación.

\[(\omega_0^2 A - A \Omega^2 - \Gamma \Omega B) \sin{\Omega t} + (\omega_0^2 B + \Gamma \Omega A - B \Omega^2 - \frac{F_0}{m}) \cos{\Omega t} = 0\]

Al igual que antes agrupo las cosas para que me queden dos factores que tienen que ser 0 independientemente.

\[(\omega_0^2 - \Omega^2) A - \Gamma \Omega B = 0\] \[\Gamma \Omega A + (\omega_0^2 - \Omega^2) B - \frac{F_0}{m} = 0\]

Volvemos a tener un sistema de 2x2 que podemos resolver.

\[A = \frac{F_0}{m} \, \frac{\Gamma \Omega}{\Gamma^2 \Omega^2 + (\omega_0^2-\Omega^2)^2}\] \[B = \frac{F_0}{m} \, \frac{(\omega_0^2-\Omega^2)}{\Gamma^2\Omega^2 + (\omega_0^2-\Omega^2)^2}\]

Lo primero que llama la atención de estas ecuaciones es la resonancia cuando \(\Omega = \omega_0\), veamos los gráficos.

m=1
F = 1
omega0 = 2
gamma = 0.5

omega = np.linspace(0,7,1000)

A = (F/m)*gamma*omega/(gamma**2 * omega**2 + (omega0**2 - omega**2)**2)
B = (F/m)*(omega0**2 - omega**2)/(gamma**2 * omega**2 + (omega0**2 - omega**2)**2)

plt.figure()
plt.plot(omega,A, label = 'A')
plt.plot(omega,B, label = 'B')
plt.plot([omega0]*2,[1.1*min(B),1.1*max(A)],'--',color = 'green') #Ploteo una linea punteada en omega0 para ver la resonancia, hablemos de esta sintaxis, acuerdense que sumar dos listas devuelve una nueva lista con la unión de las dos. Entonces multiplicar es como sumarla con sí misma, hubiese sido lo mismo escribir [omega0,omega0] pero quería mostrarles esto que suele ser útil cuando queremos una lista de algún elemento repetida muchas veces
plt.text(2.5,1,'$\omega_0$',color = 'green') #Estás son cosas que agrego para mostrarles que se pueden ir haciendo gráficos cada vez más lindos y para que sepan que estas herramientas existen. Si les confunde, no les den bola
plt.grid(True,which = 'major') #Idem lo de arriba
plt.xlabel('$\Omega$')
plt.legend(); #este ; del final lo pongo para que no aparezca un mensaje feo abajo, prueben sacarlo para ver qué pasa

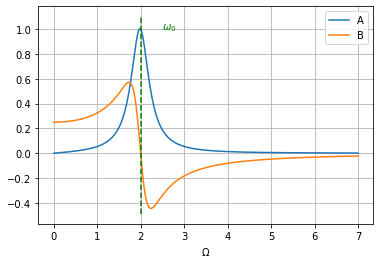
Pero qué es esto? una amplitud es negativa? Se hace 0 en \(\omega_0\)? Pero a mí me dijeron que la resonancia es cuando la amplitud crece y se rompe todo! Bueno, no, eso está pasando con A, pero no con B, es por esto que A que, en la resonancia, absorbe toda la potencia que le damos, se llama amplitud absorbente. Por otro lado, a B se le llama amplitud elástica (o dispersiva) y se la asocia con absorción de potencia instantánea. Sabemos que la potencia absorbida da cero si se la promedia en un ciclo completo.

Otra cosa que podemos ver en el gráfico es que la resonancia no está exactamente en \(\omega_0\), la amortiguación \(\Gamma\) desplaza un poco el punto de máxima intensidad (prueben buscar el \(\Omega\) que maximiza la amplitud $A$). Acá la parte analítica se las dejo a ustedes, yo les muestro lo que pasa en el gráfico cuando de a poco cambio gamma, vean que el pico se va desplazando

gamVar = np.linspace(0.6,3.9,10)
#%%
colores = np.log10(gamVar)+0.4#tiene que ir entre 0 y 1
# colors = [ cm.gnuplot(x) for x in colores]
colors = [ cm.YlGnBu(x) for x in colores]

for i in range(10):
  Avar = (F/m)*gamVar[i]*omega/(gamVar[i]**2 * omega**2 + (omega0**2 - omega**2)**2)
  plt.figure(0)
  plt.plot(omega,Avar, label = f'$\Gamma$ = {gamVar[i]:.2}', color = colors[i]) #Se dan cuenta cómo formaté el texto?
  plt.plot([omega0]*2,[1.1*min(B),1.1*max(A)],'--',color = 'green') 
  plt.text(2.02,1,'$\omega_0$',color = 'green') 
  plt.grid(True,which = 'major')
  plt.xlabel('$\Omega$')
  plt.xlim([0,4]) 

plt.legend(loc = [1,0.3]);

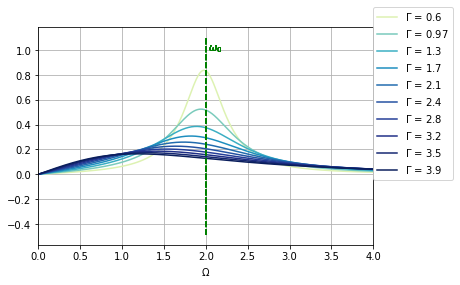
Podemos ver lo mismo pero animado, próximamente voy a subir un colab de cómo hacer estas animaciones tan bellas de forma muy simple.

Volvamos a la potencia pero pongamosle números. la potencia instantánea está dada por \(P(t) = F(t) \dot{x}_p\). Pero lo que más nos va a interesar es el promedio temporal de \(P\) durante un período esto lo escribimos como \(<P>\)

\[<P> = \frac{1}{T}\int_0^T{P(t)} dt\] \[<P> = \frac{1}{T}\int_0^T{F(t)\dot{x}_p(t)} dt\]

Donde \(T = \frac{2\pi}{\Omega}\) es el período de nuestra onda. Para poder seguir les cuento que hay unas integrales que las vamos a usar durante toda la materia. Voy a escribir acá los resultados pero ustedes tienen la tarea de hacer las cuentas y entenderlas, son cuentas en una variable que no les deberían generar problemas pero como siempre si hay dudas consulten. Un comentario extra sobre estas integrales, la importancia que tienen en la materia está muy relacionada con el uso de la base \(\{\sin, \cos\}\) para el espacio de funciones.

\(\int_0^T{\sin{\left(\frac{2\pi}{T} t\right)} \, dt} = 0\) \(\int_0^T{\cos{\left(\frac{2\pi}{T} t\right)} \, dt} = 0\) \(\int_0^T{\sin^2{\left(\frac{2\pi}{T} t\right)} \, dt} = \frac{T}{2}\) \(\int_0^T{\cos^2{\left(\frac{2\pi}{T} t\right)} \, dt} = \frac{T}{2}\) \(\int_0^T{\sin{\left(\frac{2\pi}{T} t\right)} \cos{\left(\frac{2\pi}{T} t\right)} \, dt} = 0\)

Volvamos a lo que estabamos haciendo.

\[P(t) = F_0 \cos{\Omega t}(A \Omega \cos{\Omega t} - B \Omega \sin{\Omega t})\]

Así que cuando integremos y dividamos por \(T\), usando las integrales que ahora ya conocemos, vamos a obtener

\[<P(t)> = \frac{F_0 A \Omega}{2}\]

Esta es la potencia que le estamos trasmitiendo a la masa, pero también hay una parte de la potencia que se disipa por fricción. Para calcularlo podemos hacer la misma integral de $P(t)$ en el tiempo pero en lugar de usar la potencia que usamos antes calculada con la fuerza aplicada a la masa, podemos usar la fuerza de fricción \(F_r(t) = m \Gamma \dot{x}_p\). Entonces la Potencia disipada queda

\[<P_{fr}(t)> = \frac{1}{T}\int_0^T{m \Gamma \dot{x}^2_p} \, dt\]

Igual que antes, integramos, dividimos por \(T\) y obtenemos \(<P_{fr}(t)> = \frac{1}{2}m \Gamma \Omega^2 (A^2 + B^2)\).

La guía nos dice que verifiquemos la igualdad de estas dos ecuaciones pero antes pensemos ¿por qué deberían ser iguales? En el régimen estacionario estamos haciendo una fuerza sobre la masa (realizando trabajo) y el movimiento es siempre el mismo. Si se disipara más de lo que se trasmite, la masa debería oscilar cada vez menos, si se trasmitiera más de lo que se disipa, la masa debería oscilar cada vez con más energía. Veamos qué nos dice Python.

P = F*A*omega/2
Pfr = 0.5*m*gamma*omega**2*(A**2+B**2)

plt.plot(omega,P, '--',label = 'Potencia transmitida')
plt.plot(omega,Pfr,'-.', label = 'Potencia disipada')
plt.plot(omega, P - Pfr, label = 'Diferencia entre potencias')
plt.grid() 
plt.xlabel('$\Omega$')
plt.ylabel('Potencia')
plt.legend(); #este ; del final lo pongo para que no aparezca un mensaje feo abajo, prueben sacarlo para ver qué pasa

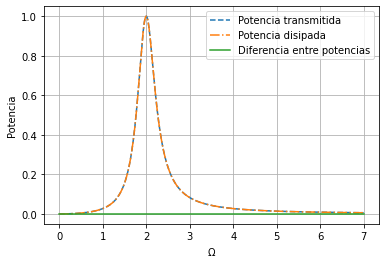
Lo logramos! ahora les queda a ustedes comprobarlo analíticamente. Fijense que la curva azul quedó abajo de la naranja, eso se ve en la verde que es constantemente 0. Justo lo que esperabamos.

Seguramente ya les habrán contado muchas cosas y mostrado muchos videos de cosas que se rompen por resonancia, sino les dejo algunos videitos del puente de Tacoma y de un helicoptero que se rompe. La resonancia es un tema que va a aparecer un montón en la carrera y la idea es tan simple como la que acaban de ver (aunque las cuentas no tanto). ¿Se les ocurre porqué estas cosas se rompen? Piensenlo y nos lo cuentan por el campus.