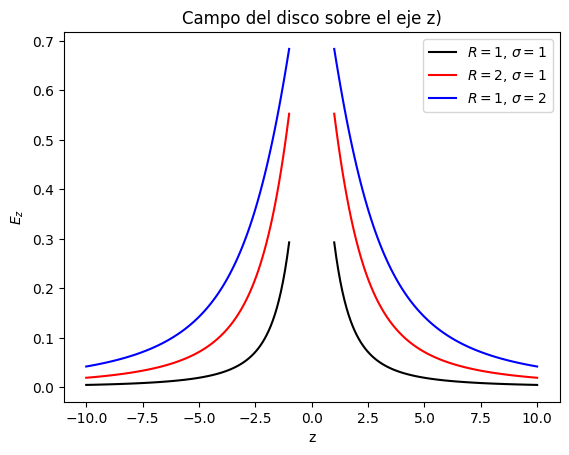
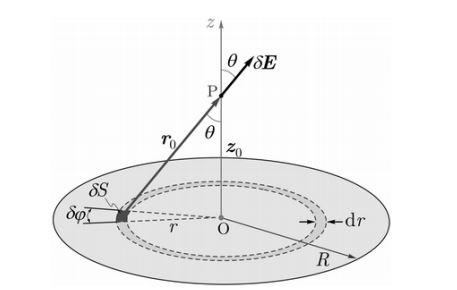
En esta ocasión vamos a calcular el campo eléctrico que produce un disco homogéneo de radio $R$ con densidad superficial $\sigma$ constante, en los puntos del espacio a lo largo del eje del disco (Es decir, el campo sobre el eje z de la figura. La figura sale del Libro de Roederer).
Para esto debemos utilizar el método de integración directa para el calculo del campo eléctrico.
Recordemos que el campo eléctrico para una distribución superficial de carga se puede calcular según la integral \begin{equation} \vec{E}(\vec{r}) = \frac{1}{4\pi\epsilon_0} \int_{S} \frac{\sigma(\vec{r}’)(\vec{r} - \vec{r}’)}{\Vert \vec{r} - \vec{r}’\Vert^3}dS’ \end{equation}
Ahora, un cachito de disco, por ejemplo el diferencial $\delta S$ de la figura, producirá un cierto campo $\delta \vec{E}$ sobre el eje z, además va a tener la dirección del vector que une a $\delta S$ con ese punto del espacio, digamos el $\vec{P}$ de la figura, cuya distancia a $\delta S$ estará dada por $\vec{r}_0$.
Entonces, debemos preguntarnos ¿Quién es $\delta S$? para así conocemos quien es $\delta \vec{E}$.
Podemos observar que \(\delta S = r dr d\varphi\)
Por otro lado, el modulo de $\vec{r}_0$ es \(\Vert \vec{r}_0 \Vert = r_0= \sqrt{r^2 + z_0}\)
Por definición, el modulo de un campo $\vec{E}$ esta dado por \(\Vert \vec{E} \Vert = \frac{1}{4\pi\epsilon_0} q_f \frac{\vec{r_p} - \vec{r_f}}{\Vert\vec{r_p} - \vec{r_f}\Vert^2}\)
donde naturalmente $\vec{r_p}$ es la posición del punto campo y $\vec{r_f}$ la de la fuente, siendo $q_f$ la fuente del campo.
Nos quedan por identificar entonces, quien es $\vec{r_p} - \vec{r_f}$.
$\vec{r_f}$: son todos los puntos fuente, o sea $\vec{r_f}$$=(r’ \cos{\varphi},r’ \sin{\varphi} ,0)$
$\vec{r_p}$: son todos los puntos de prueba, en este caso habiamos tomado el eje $z$, por ende $\vec{r_p} = (0,0,z)$
En conclusión, nos queda para resolver la siguiente integral \(\vec{E}(\vec{0,0,z}) = \frac{1}{4\pi\epsilon_0} \int_{0}^{R} \int_{0}^{2\pi} \sigma \frac{(r' \cos{\varphi},r' \sin{\varphi} ,0) - (0,0,z)}{\Vert (r' \cos{\varphi},r' \sin{\varphi} ,0) - (0,0,z) \Vert^3} r dr d\varphi\)
¿Es un asquito, no?
En realidad, no es tan terrible, solo asusta un poco y sale.
Peeeero, podemos pedirle ayuda a python.
Python tiene una librería que se llama Sympy (cuya documentación esta acá) que tiene un montón de herramientas para calculo simbólico y en particular, podemos definir la integral a integrar e integrarla. Pero, hay que tener un toque de cuidado, porque no es simplemente poner los datos y punto, hay que hacer una pequeña interpretación de lo que debemos hacer.
Veamos como es esto. Primero importemos lo necesario.
%matplotlib inline
import sympy as sym
# Primero definimos as variables y le asignamos un simbolo.
# La nomenclatura suele coincidir con la de Latex
R, r_f, varphi_f, x, y, z, kappa_e, sigma = sym.symbols("R, r_f, varphi_f, x. y, z, kappa_e, sigma")
# Calculo la diferencia entre las posiciones de los puntos campo y fuente
# r_p - r_f = (Dx, Dy, Dz)
Dx = (-r_f * sym.cos(varphi_f))
Dy = (-r_f * sym.sin(varphi_f))
Dz = z
# Calculemos la norma al cubo de r_p - r_f
norma = (Dx**2 + Dy**2 + Dz**2)**(3/2)
# Por ultimo, construimos el campo de cada componente
E_x = kappa_e * sigma * Dx/norma
E_y = kappa_e * sigma * Dy/norma
E_z = kappa_e * sigma * Dz/norma
#Veamos como quedo cada componente
# Campo en x
E_x
$\displaystyle - \frac{\kappa_{e} r_{f} \sigma \cos{\left(\varphi_{f} \right)}}{\left(r_{f}^{2} \sin^{2}{\left(\varphi_{f} \right)} + r_{f}^{2} \cos^{2}{\left(\varphi_{f} \right)} + z^{2}\right)^{1.5}}$
# Campo en y
E_y
$\displaystyle - \frac{\kappa_{e} r_{f} \sigma \sin{\left(\varphi_{f} \right)}}{\left(r_{f}^{2} \sin^{2}{\left(\varphi_{f} \right)} + r_{f}^{2} \cos^{2}{\left(\varphi_{f} \right)} + z^{2}\right)^{1.5}}$
# Campo en z
E_z
$\displaystyle \frac{\kappa_{e} \sigma z}{\left(r_{f}^{2} \sin^{2}{\left(\varphi_{f} \right)} + r_{f}^{2} \cos^{2}{\left(\varphi_{f} \right)} + z^{2}\right)^{1.5}}$
No es tan dificil, no? Y quedan espectaculares, parece que nos entiende a la perfección.
Ahora resta hacer las integrales. Podemos ver como es el uso de Integrate en este link.
Recordemos que es una integral doble, una sobre $r_f$ con limites $[0, R]$ y otra sobre toda la circunferencia del disco cargado, o sea sobre $\varphi_f \in [0, 2\pi)$.
Codiemos una a una y veamos las soluciónes
# Primero hacemos la integral de la componente E_x
sym.integrate(E_x * r_f, (varphi_f, 0, 2*sym.pi), (r_f, 0, R))
$\displaystyle 0$
# Primero hacemos la integral de la componente E_y
sym.integrate(E_y * r_f, (varphi_f, 0, 2*sym.pi), (r_f, 0, R))
$\displaystyle 0$
# Primero hacemos la integral de la componente E_z
sym.integrate(E_z * r_f, (varphi_f, 0, 2*sym.pi), (r_f, 0, R))
$\displaystyle - \frac{2.0 \pi \kappa_{e} \sigma}{\left(\frac{R^{2}}{z^{2}} + 1\right)^{0.5}} + 2.0 \pi \kappa_{e} \sigma$
Listo, tenemos la solución al campo. Este sera \(\vec{E}(0,0,z)= \left(0, 0, 2\pi k_e \sigma \left( 1-\frac{1}{\sqrt{R^2z^{-2} + 1}} \right) \right)\) Es, decir \(E_z(0,0,z) = 2\pi k_e \sigma \left( 1-\frac{1}{\sqrt{R^2z^{-2} + 1}} \right)\)
Ya que estamos, hagamos una grafica del campo en función de $z$ para darnos una idea de lo que pasa.
Tomemos radio $R=1$
import numpy as np
import matplotlib.pyplot as plt
# Definimos una funcion para el campo
def E_disco(z,R=1,sigma=1):
"""Calcula el campo del disco
parameters:
z : Coordenada z
R : Radio del disco
return Campo del disco
"""
raiz = ((R**2/z**2) + 1) ** (1/2)
#e_0 = 8.85*(10**-12)
#k_e = 1/(4 * np.pi * e_0)
E = sigma * (1-(1/raiz))
return E
# Defino valores para z
z = np.linspace(1, 10, 100)
E_1 = E_disco(z, 1, 1)
E_2 = E_disco(z, 2, 1)
E_3 = E_disco(z, 3, 1)
plt.plot(z, E_1,'k', z, E_2, 'r', z, E_3,'b')
plt.plot(-z, E_1,'k', -z, E_2, 'r', -z, E_3,'b')
plt.xlabel('z')
plt.ylabel(r'$E_z$')
plt.title('Campo del disco sobre el eje z)');
plt.legend([r'$R=1$, $\sigma=1$', r'$R=2$, $\sigma=1$', r'$R=1$, $\sigma=2$']);
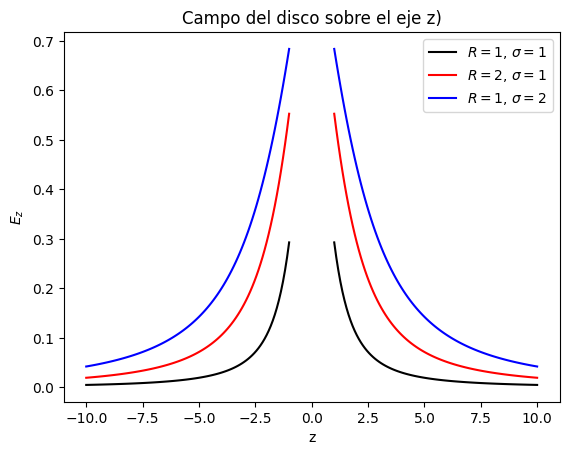
Se puede apreciar que a medida que el radio del disco es mas grande, el campo es mas intenso. Sin embargo, a medida que nos alejamos del disco, el campo decae con el cuadrado de la distacia.
Por otro lado, podemos ver que sobre el disco (recordar que es un disco sin espesor, porlo que esta en z=0) el campo tiende a infinito.
# Defino valores para z
z = np.linspace(1, 10, 100)
E_1 = E_disco(z, 1, 1)
E_2 = E_disco(z, 1, 2)
E_3 = E_disco(z, 1, 3)
plt.plot(z, E_1,'k', z, E_2, 'r', z, E_3,'b')
plt.plot(-z, E_1,'k', -z, E_2, 'r', -z, E_3,'b')
plt.xlabel('z')
plt.ylabel(r'$E_z$')
plt.title('Campo del disco sobre el eje z)');
plt.legend([r'$R=1$, $\sigma=1$', r'$R=2$, $\sigma=1$', r'$R=1$, $\sigma=2$']);
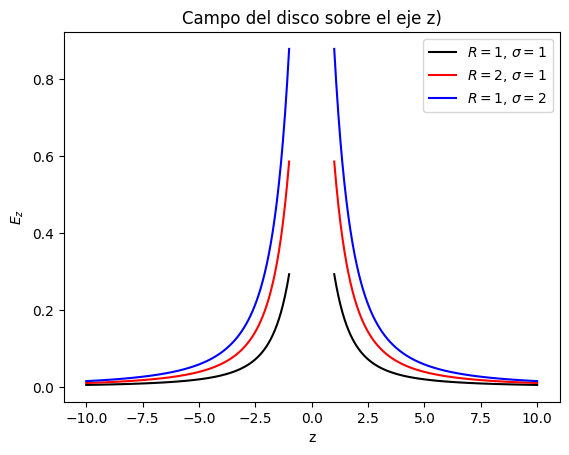
Respecto a la densidad de carga tenemos la misma tendencia. Es decir, tambien a medida que la densidad de carga (es decir la carga total del disco) es más grande, la intensidad del campo sera mayor.