TP - Aeropuertos
Ley de Benford
Grupo 8: Cosarinsky Matias, Remus Ezequiel
Ley de Benford
Por curiosidad pensamos ver si las distancias recorridas por los vuelos siguen la ley de Benford. Para ello tomamos los valores los valores no repetidos entre todas las y graficamos la frecuencia de su primer dígito.
library(ggplot2)#Benford's Law
# Leo el csv con los datos
df.vuelos <- read.csv("./csv/vuelos_2021.csv")
#tomamos las distancias positivas y nos quedamos con los valores unicos
distancias_pos <- df.vuelos$distancia.km.x[which(df.vuelos$distancia.km.x > 0)]
unicas.dist <- unique(as.integer(distancias_pos))
length(unicas.dist)
## [1] 208
#dividimos en los dígitos(transformando primero en un vector de caracteres) y nos quedamos con el primero usando function(x) x[1]
primer.digito.unicos <- sapply(strsplit(as.character(unicas.dist), split=''), function(x) x[1])
#ahora construimos un data frame con las proporciones de los dígitos
df.dist <- as.data.frame(prop.table(table(primer.digito.unicos)))
df.dist$primer.digito.unicos <- as.integer(df.dist$primer.digito.unicos)
y <- function(x) log(1+1/x, 10)
#realizamos el gráfico
ggplot(df.dist, mapping=aes(x=primer.digito.unicos, y=Freq)) +
geom_bar(stat='identity', fill='blue') +
labs(x='Dígito', y='Proporción de apariciones', title='Ley de Benford en distancias') +
theme(plot.title = element_text(hjust = 0.5))+
geom_line(mapping = aes(y = y(primer.digito.unicos)),size=1.3) +
scale_x_continuous(breaks=1:9, labels=c('1','2','3','4','5','6','7','8','9'))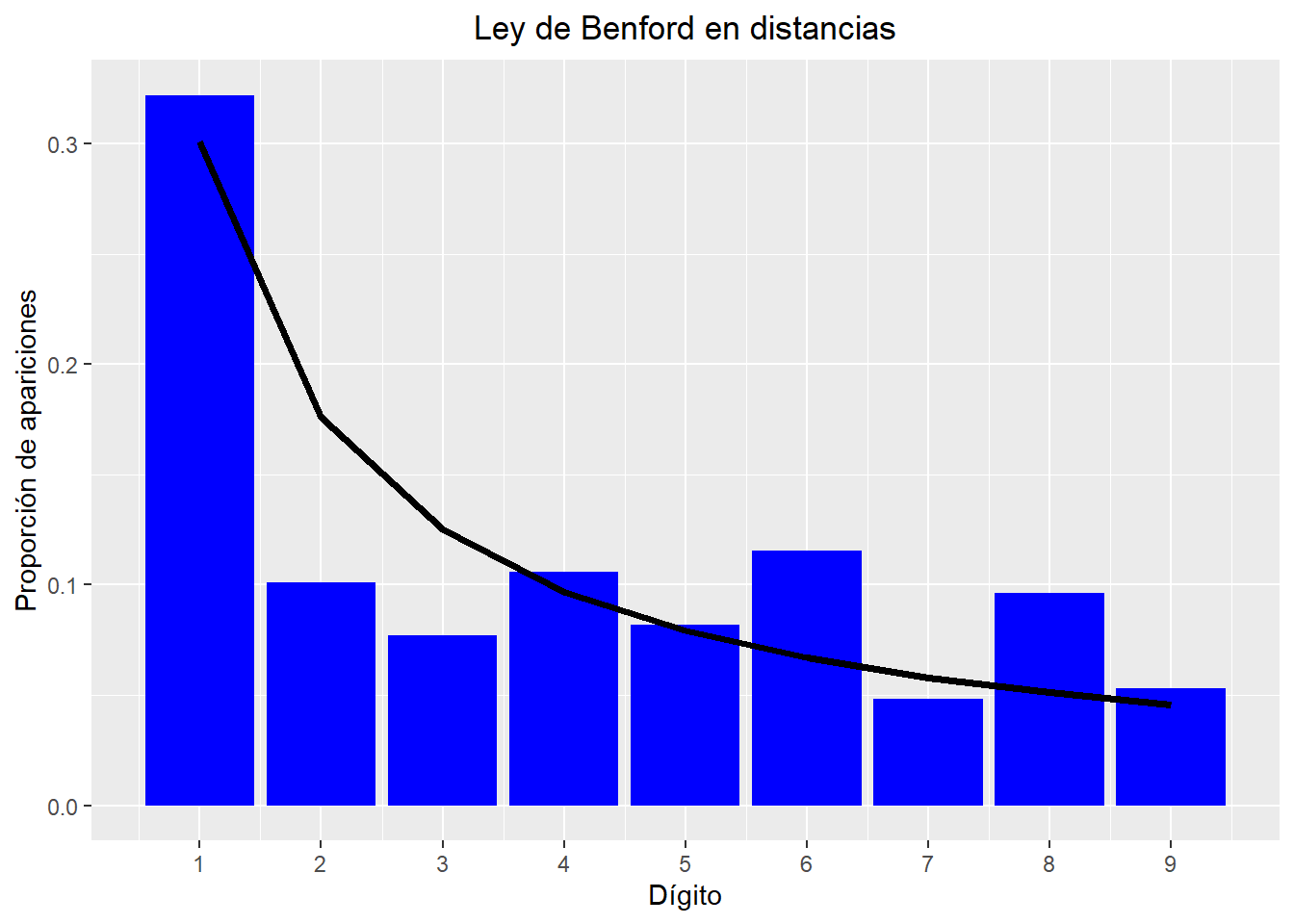 A partir del gráfico podemos ver que la distancia recorrida por los vuelos, que vendría a ser la distancia entre dos ciudades, se adapta bastante bien a lo establecido por la ley de Benford, salvo para los dígitos 5,7 y 9 que aparecen en mayor proporción a lo esperado.
A partir del gráfico podemos ver que la distancia recorrida por los vuelos, que vendría a ser la distancia entre dos ciudades, se adapta bastante bien a lo establecido por la ley de Benford, salvo para los dígitos 5,7 y 9 que aparecen en mayor proporción a lo esperado.
Tenemos 208 distancias diferentes, puede que con más observaciones este comportamiento sea aún más evidente pero para esto necesitaríamos vuelos entre ciudades de más países.